Understanding Matrixes And Submatrixes

Prior to encountering this problem, I have never worked with matrixes before. Reading through it and exploring the sample inputs, at first I only understood them to be an array of arrays. But as to how to move elements of one array so that they would end up in a desired position, or how to move them around several times to achieve the same, it was something really new to me.

So I approached the problem by first reading about matrixes and studying other people's published blogs about it. Some were really instructive and helpful. Here, I would like to present my own solution to the Hacker Rank problem entitled Flipping Matrix.

The Problem

You are given a 2n x 2n matrix with each cell containing an integer. A sample input looks like this:

let matrix1 = [
[112, 42, 83, 119],
[56, 125, 56, 49],
[15, 78, 101, 43],
[62, 98, 114, 108]
]

Each quadrant (n x n) would contain the following integers:

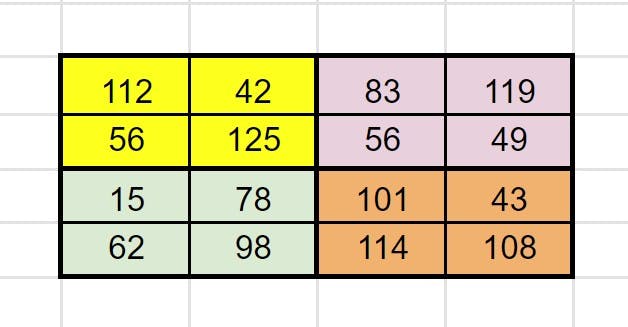
• Upper-left: 112, 42, 56, 125
• Upper-right: 83, 119, 56, 49
• Lower-left: 15, 78, 62, 98
• Lower-right: 101, 43, 114, 108

You can reverse any of the rows or columns any number of times so that the sum of the elements in the upper-left quadrant is maximal.

The Algorithm

The reversing of rows and columns basically all boils down to this idea: each integer in the upper-left quadrant can be replaced or retained, provided they are the highest possible integer that can be placed in their position after comparing them with other candidates in the other quadrants.

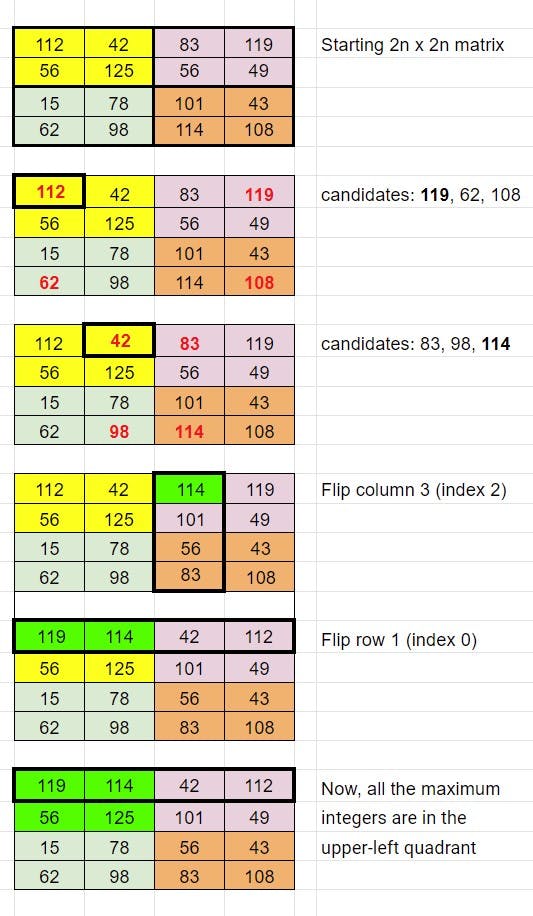
To illustrate, the candidates for 42's position are 83, 98, and 114. Since 114 is the highest integer among them, you flip column 3 so 114 will be moved to row 1.

Notice that both 114 and 119 are now in the same row, and they are both the highest candidates for the original positions of 112 and 42.

So to get them to the upper-left quadrant, you flip the row once again.

Here, 56 and 125 will stay in their positions because they are already the highest integers among their respective candidates, as follows:

• 56: 49, 15, 43
• 125: 56, 78, 101

Thus, after all the strategic reversing is made, the integers that will be in the upper-left quadrant are 119, 114, 56, and 125, which would return the maximal sum of 414.

The Code

Now, how to put this into code? I started by having a reference to the matrixes. I declared a variable referring to the length of the entire matrix, and then another variable referring to the length of the sub-matrixes, which is basically half of the length of the entire matrix.

  let matrixL = matrix.length
  let submatrixL = matrix.length / 2

I also needed, a variable to hold the total of the integers that would end up in the upper-left quadrant.

  let total = 0

I, then, proceeded to identify first an integer currently in the upper-left quadrant. For instance, 112 here would be matrix[r][c], or matrix[0][0]. Here, it helps to have a good grasp of the concepts of arrays in relation to zero-indexing.

Then I went on to identify the 3 candidates against which I will compare the current integer. The candidates that could possibly replace 112 have the following indexes:

• 119: matrix[r][matrixL - c - 1], or here specifically, matrix[0][3]
• 62: matrix[matrixL - r - 1][c], or here specifically, matrix[3][0]
• 108: matrix[matrixL - r - 1][matrixL - c - 1], or here specifically, matrix[3][3]

First, I used Math.max to return the largest of the numbers between the current integer and an initial max number set using Number.NEGATIVE_INFINITY. This is so that I have a starting input parameter to compare the first resulting number to.

Number.NEGATIVE_INFINITY can include negative numbers, so it is a wise property to use because it makes the code more scalable, as opposed to using Number.MIN_VALUE, which would not account for cases wherein negative numbers are included as inputs.

As the iteration moves from one integer to the next in the upper-left quadrant, the candidates also change respectively, each time making a comparison and finding the greatest possible candidate.

By iterating through this process for each original integer in the upper-left quadrant, I was able to arrive at a set of numbers that would provide the maximum possible sum.

function flippingMatrix(matrix) {
  let matrixL = matrix.length
  let submatrixL = matrix.length / 2
  let total = 0

  for (let r = 0; r < submatrixL; r++) {
    for (let c = 0; c < submatrixL; c++) {
      let max = Number.NEGATIVE_INFINITY 

      max = Math.max(matrix[r][c], max)    
      max = Math.max(matrix[r][matrixL - c - 1], max) 
      max = Math.max(matrix[matrixL - r - 1][c], max)  
      max = Math.max(matrix[matrixL - r - 1][matrixL - c - 1], max)  

      total += max
    }
  }

  return total
}

Key Methods & Challenges

In this exercise, I was able to practise applying a more complex for loop to a problem and correctly identifying indexes using columns and rows. In addition, I found it a challenge to make code scalable, meaning not hard-coding lengths and rows and columns. After careful thought and exploration, I was able to come up with code that works just fine regardless of the size of the sub-matrixes.